nLab quantum reader monad

Idea

By the linear reader monad or quantum reader monad we shall mean the reader monad but on the category of vector spaces (in applications specifically of complex vector spaces, though essentially all discussion here applies over any ground field):

$$B \,\colon\, Set \;\;\;\;\; \vdash \;\;\;\;\; \bigcirc_B \;\coloneqq\; Map(B,-) \;=\; \underset{B}{\prod}(-) \;\colon\; Vect \to Vect \,.$$

The reason for the quantum physics-terminology is that this monad is closely related to — in fact arguably is the fundamental formalization in categorical logic of — the concept of quantum measurement, including its subtle peculiarities such as the dependence on a choice of measurement basis and the phenomenon of wavefunction collapse entailed by the measurement process. It would in fact make good sense to speak of the quantum measurement monad — but notice that the conceptual difference between “reading” (say a global parameter, as is common interpretation for the reader monad when used as a monad in computer science) and “measuring” is small already informally and seems to all but vanish in the modal logic of the quantum reader (its “quantum modal logic”, if you wish).

Often one is interested in the case that the parameter set $B$ here is a finite set (explicitly so in applications to quantum information theory and quantum computing where eg. $B =$ Bool for qbits, but it could probably be argued that any real measurement in experiment can only ever resolve a finite set of potential outcomes), and this is the case we shall focus on now unless otherwise specified.

In this case of finite parameter set $B$, the existence of biproducts in VectorSpaces — namely of direct sums $\oplus_B$ — implies that the underlying functor of the quantum $B$-reader monad coincides with that of the $B$-coreader comonad $\star_B \;\coloneqq\; \coprod_B (-) \;\colon\; Vect \to Vect$:

(1)$$\array{ \star_B \mathscr{V} &\simeq& \oplus_B \mathscr{V} &\simeq& \bigcirc_B \mathscr{V} \\ && \simeq \\ && \mathbb{1}^B \otimes \mathscr{V} } \,.$$

In fact, the induced joint monad- and comonad-structure on this functor are compatible to jointly make the quantum reader be a Frobenius monad:

An organized way to see this Frobenius monad-structure on the quantum reader monad over a finite parameter set is to observe (which is a straightforward inspection, but we spell it out below) that the quantum $B$-reader monad is also isomorphic to the $\mathbb{1}^B$-writer monad corresponding to the associative algebra

(2)$$\mathbb{1}^B \;=\; \oplus_B k \;\in\; CMon\big(Vect_k\big) \,=\, CAlg_k \,,$$

which is generated by a $B$-indexed set of mutually orthogonal projection operators $\{P_b\}_{b \colon B}$ (over the ground field $k$).

It is immediate to check that (2) canonically carries the further structure of a Frobenius algebra (see the example there) with coproduct $\delta \;\colon\; \mathbb{1}^B \to \mathbb{1}^B \otimes \mathbb{1}^B$ given by duplication over the $B$-basis: $\delta \;\colon\; P_b \,\mapsto\, P_B \otimes P_b$. But this makes manifest that the underlying functor of tensoring $\mathbb{1}^B \otimes (-)$ also carries the structure of a comonad in a compatible way to make a Frobenius monad.

(3)

In this its incarnation as the $\mathbb{1}^B$-writer Frobenius monad, the quantum $B$-reader monad is famous in the literature on quantum information theory via dagger-compact categories as encoding quantum measurement with respect to the $B$-basis – known as classical structures or Frobenius structures in these references [Coecke & Pavlović (2008), §1.5.1, Coecke & Paquette (2008), §2.3], as well as classically controlled quantum gates [Heunen & Vicary (2019), around Lem. 5.61, albeit not making the monadic algebra explicit] (See also at no-cloning theorem this Remark.)

In this guise, the quantum reader monad is reflected by the “green spiders” in the ZX-calculus.

Properties

Relation to dependent linear types

We discuss the quantum reader monad as the reader monad induced by $B$-dependent linear types which have biproducts, such as $B$-indexed sets of vector spaces. Notation and graphics follows CQTS (2022).

Proposition

(quantum $\bigcirc_B$-algebras are $B$-dependent linear types)
For $B \;\in\;$ FiniteSets, the category of algebras for the $B$-reader monad

$$\array{ \bigcirc_B \colon & Vect &\xrightarrow{\phantom{---}}& Vect \\ & \mathscr{H} &\mapsto& Maps\big(B, \mathscr{H} \big) \mathrlap{ \; \simeq \; \underset{b \colon B}{\bigoplus} \mathscr{H} } }$$

on the category Vect of vector spaces (over any given ground field) is equivalent to that of vector bundles over $B$ (hence to $B$-indexed sets of vector spaces):

$$Vect^{\bigcirc_B} \;\;\simeq\;\; Vect_B \,.$$

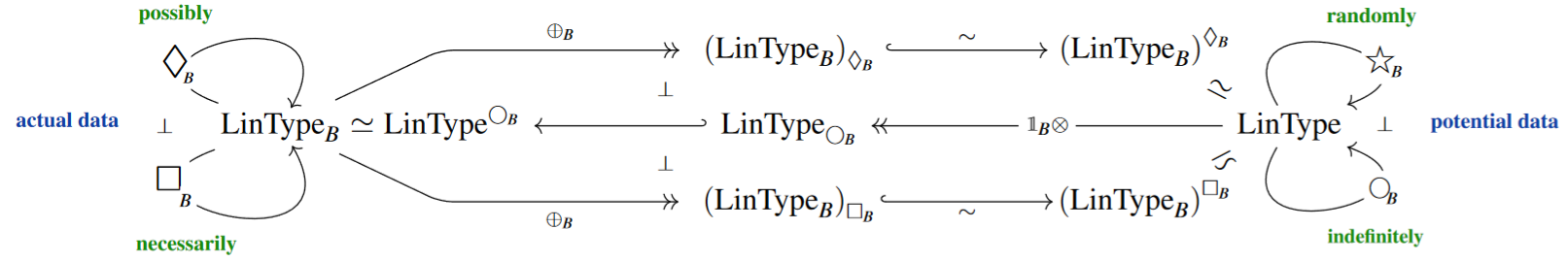
(Something close to this statement, in its adjoint form for the quantum coreader comonad $\bigstar$, is the content of Coecke & Pavlović 2008, Thm. 1.5.)

Proof

We state first an abstract proof and then a concrete proof.

Abstractly, observe that Vect has (finite) biproducts (given by the direct sum of vector spaces) which together with the assumption that $B$ is finite implies that $\underset{B}{\prod} \;\colon\; Vect_B \xrightarrow{\;} Vect$:

1. is not only a right adjoint but also a left adjoint (hence an ambidextrous adjoint to pullback of vector bundles along $B \to \ast$), hence in particular it preserves all colimits;

2. is a conservative functor (since the $B$-components of any morphism of vector bundles over $V$ can still be extracted via (co-)projections from their image under forming the biproduct over $B$).

Therefore the conditions for the monadicity theorem are met (see there), implying that the functor is monadic functor, which in turn implies the claim.

Alternatively, we now check the claim more concretely by unwinding what it means for a vector space to carry $\bigcirc_B$-algebra structure and for a linear map between vector spaces to be a homomorphism for this structure:

First observe that the $\bigcirc_B$-monad product $join^{\bigcirc_B} \;\colon\; \bigcirc_B \bigcirc_B \xrightarrow{join^{\bigcirc}} \bigcirc_B$ on a vector space $\mathscr{H} \,\in\, Vect$ is explicitly given by:

$$\array{ \underset{b \colon B}{\bigoplus} \; \underset{b' \colon B}{\bigoplus} \; \mathscr{H} & \xrightarrow{\;\; join^{\bigcirc}_{\mathscr{H}} \;\;} & \underset{b'' \colon B}{\bigoplus} \mathscr{H} \\ \big( \psi_{b,b'} \big)_{b,b' \colon B} &\mapsto& \big( \psi_{b'' ,b''} \big)_{b'' \colon B} }$$

and that a $\bigcirc_B$-algebra structure on $\mathscr{H}$ is a linear map of this form:

(4)$$\rho^\bigcirc_{\mathscr{H}} \;\colon\; \underset{b \colon B}{\oplus} \mathscr{H} \xrightarrow{\phantom{-}(P_b)_{b \colon B}\phantom{-}} \mathscr{H} \,.$$

Of such maps, the $\bigcirc_B$-action property (here) demands that the following two linear maps are equal:

$$\array{ & \underset{b \colon B}{\bigoplus} \; \underset{b' \colon B}{\bigoplus} \; \mathscr{H} &\xrightarrow{\; join^\bigcirc_{\mathscr{H}} \;}& \underset{b'' \colon B}{\bigoplus} \mathscr{H} &\xrightarrow{\; \rho^\bigcirc_{\mathscr{H}} \;}& \mathscr{H} \\ & \big( \psi_{b,b'} \big)_{b,b' \colon B} &\mapsto& \big( \psi_{b'',b''} \big)_{b'',b'' \colon B} &\mapsto& \underset{b'' \colon B}{\sum} P_{b''}(\psi_{b'',b''}) \\ \text{and} & \\ & \underset{b \colon B}{\bigoplus} \; \underset{b' \colon B}{\bigoplus} \; \mathscr{H} &\xrightarrow{\; \bigcirc \rho^\bigcirc_{\mathscr{H}} \;}& \underset{b'' \colon B}{\bigoplus} \mathscr{H} &\xrightarrow{\; \rho^\bigcirc_{\mathscr{H}} \;}& \mathscr{H} \\ & \big( \psi_{b,b'} \big)_{b,b' \colon B} &\mapsto& \big( \underset{b \colon B}{\sum} P_{b}(\psi_{b,b'}) \big)_{b' \colon B} &\mapsto& \underset{b, b' \colon B}{\sum} P_{b'}\big(P_{b}(\psi_{b,b'})\big) \mathrlap{\,.} }$$

By considering the value of these maps on tuples of vectors $\big(\psi_{b,b'}\big)_{b,b' \colon B}$ which are non-zero only for single elements $(b,b') \in B \times B$ one finds that the above condition is equivalent to the following condition:

$$\underset{ b, b' \colon B }{ \forall } \;\;\;\; P_b \circ P_{b'} \;=\; \left\{ \array{ P_b &\text{if} \; b = b' \\ 0 & \text{otherwise} \,. } \right.$$

Moreover, the $\bigcirc_B$-unit $\id \xrightarrow{\;\; ret^{\bigcirc_B} \;\;} \bigcirc_B$ is given by the diagonal map into the biproduct

$$\array{ \mathscr{H} &\xrightarrow{\;\; ret^{\bigcirc_B}_{\mathscr{H}} \;\;} & \underset{b \colon B}{\bigoplus} \mathscr{H} \\ \psi &\mapsto& (\psi_b \coloneqq \psi)_{b \colon B} }$$

so that the unitality property (here) of the $\bigcirc_B$-algebra structure $(P_b)_{b \colon B}$ demands equivalently that the composite

$$\array{ \mathscr{H} &\xrightarrow{\; ret^{\bigcirc_B}_{\mathscr{H}} \;}& \underset{b \colon B}{\bigoplus} \mathscr{H} &\xrightarrow{\; \rho^{\bigcirc_B}_{\mathscr{H}} \;}& \mathscr{H} \\ \psi &\mapsto& \big( \psi \big)_{b \colon B} &\mapsto& \underset{b \colon B}{\sum} \; P_b(\psi) }$$

is the identity function on $\mathscr{H}$, hence that this system of projection operators is “complete” in that

$$\underset{b \colon B}{\bigoplus} P_b \;=\; id_{\mathscr{H}} \,.$$

In summary, this means that for $B$-tuples of linear maps $(P_b \colon \mathscr{H} \to \mathscr{H})_{b \colon B}$ as in (4) to constitute a $\bigcirc_B$-module structure is equivalent to them being systems of orthogonal linear projection operators, whose images

$$\mathscr{H}_b \;\coloneqq\; im(P_b) \;\subset\; \mathscr{H}$$

span$\;$ $\mathscr{H}$ under direct sum:

$$\mathscr{H} \;\simeq\; \underset{b \colon B}{\bigoplus} \mathscr{H}_b \,.$$

Such structures, of course, are exactly the images under the right base change $\underset{B}{\prod} \;\colon\; Vect_B \longrightarrow{\;} Vect$ of $B$-indexed sets of vector spaces.

Finally, the homomorphism-property on a linear map $\mathscr{H} \xrightarrow{\phi} \mathscr{H}'$ between the underlying vector spaces of two such $\bigcirc_B$-modules demands that the following diagram commutes:

$$\array{ \underset{b \colon B}{\bigoplus} \mathscr{H} &\xrightarrow{\;\;\; \underset{b \colon B}{\oplus} \;\;\;}& \underset{b \colon B}{\bigoplus} \mathscr{H} \\ \mathllap{ {}^{ \big( P_b \big)_{b \colon B} } } \big\downarrow && \big\downarrow \mathrlap{ {}^{ \big( P'_b \big)_{b \colon B} } } \\ \mathscr{H} & \underset{\phantom{---} \phi \phantom{---} } {\longrightarrow} & \mathscr{H}' \,. }$$

The $B$-indexed components of this condition require that $\phi$ commutes with all these projection operators, in that

$$b \colon B \;\;\;\; \vdash \;\;\;\; P'_b \circ \phi \;=\; \phi \circ P_b \,.$$

But this evidently means that $\phi$ itself is the image under the direct sum-functor

$$\phi \;=\; \underset{b \colon}{\oplus} \phi_b$$

of a $B$-tuple of linear maps between the $B$-indexed component spaces:

$$b \colon B \;\;\; \colon \;\;\; \mathscr{H}_b \longrightarrow \mathscr{H}' \,.$$

This is the defining property of morphisms in $Vect_B$ and hence shows that $\bigcirc_B$-algebra homomorphisms are equivalently morphisms of $B$-indexed sets of vector spaces, hence that the two categories are agree.

Example

(free quantum $\bigcirc_B$-algebras and quantum measurement bases)
The free $\bigcirc_B$-algebras in Vect are those whose underlying vector space is of the form $\bigcirc_B \mathscr{B} = \underset{b \colon B}{\bigoplus} \mathscr{B}$ for any $\mathscr{B} \,\in \, Vect$, hence, under the equivalence of Prop. , are those $B$-dependent linear types which happen to assign the same vector space $\mathscr{B}$ for all $b \colon B$.

But homomorphisms of such free $\bigcirc_B$-algebras are still allowed to be non-trivially $B$-dependent families of linear maps. This is directly a special case of Prop. but is also immediate under the Kleisli equivalence from observing that $\bigcirc_B$-Kleisli morphisms are of the following form:

$$\array{ \mathscr{B} &\xrightarrow{ \big( \phi_b \big)_{b \colon B} }& \underset{b \colon B}{\bigoplus} \mathscr{B}' \,. }$$

Relation to quantum measurement

In quantum information theory the $\bigcirc_B$-algebras in complex vector spaces which are free on the tensor unit $\mathbb{C} \,\in\, \mathbb{C} Vect$ (the 1-dimensional complex vector space) play the role of (finite dimensional complex vector spaces underlying) finite-dimensional Hilbert spaces of quantum states which are spanned by the set $B$ regarded as a “quantum measurement basis”.

For example, the dependent linear type of qbits is the free $\bigcirc_B$-algebra $\bigcirc_{Bool} \mathbb{C}$ spanned by the classical type Bool $= \{0,1\}$ of bits, reflecting the two canonical quantum measurement-outcomes ($\vert 0\rangle$, $\vert 1 \rangle$) of qbits.

Curiously, from this one finds that quantum measurement is exactly indefiniteness handling

where

• “indefiniteness” is understood as the the effect/modality expressed by the reader monad $\bigcirc_B$ (see here),

• “handling” is understood as effect handling in the sense of effect-monads in computer science (see here);

namely:

Notice that this process may be understood as the “dynamic lifting” of quantum measurement-results into the context (here: $B =$ Bool) of the ambient dependent linear type theory.

For more on this see at quantum circuits via dependent linear types.

This naturally relates to the discussion of quantum measurement via Frobenius algebra-structures which is popular in the context of quantum information theory via dagger-compact categories – as follows:

Remark

(quantum reader monad is Frobenius)
Since the direct sum of vector spaces is a biproduct and using our running assumption that $B$ is a finite set, it follows that the underlying functor of the quantum reader monad from Prop. coincides with that of the coreader comonad, and hence that the quantum reader monad is a Frobenius monad (see there).

Remark

(quantum reader monad is special Frobenius writer monad)
Consider the $B$-indexed the direct sum $k^{\otimes^B}$ of the ground field with itself as a $k$-algebra and write

$${k^{\otimes^B}}\text{-}Writer \;\colon\; Vect \to Vect$$

for the writer monad corresponding to this monoid object in Vect: The monad which acts by forming the tensor product $Writer_{k^{\otimes^B}}(V) \;\coloneqq\; V \otimes \big( k^{\otimes^B} \big)$ and whose monad multiplication and unit of a monad are induced from the multiplication and unit in this monoid.

The above proof of Prop. shows at once that this writer monad is isomorphic to the $B$-reader monad:

$$\bigcirc_B \;\simeq\; Writer_{k^{\otimes^B}} \,.$$

Now the monad modules over a writer monad are just the ordinary modules over the corresponding monoid, so that

$$\bigcirc_B Mod(Vect) \;\simeq\; \big( k^{\otimes^B} \big)Mod(Vect) \,.$$

This provides a rather transparent re-derivation of and alternative perspective on Example .

Dually, as in Prop. , the quantum coreader comonad is isomorphic to the coreader comonad corresponding to the coalgebra-structure on $k^{\otimes^B}$.

Hence, as a Frobenius monad (Prop. ), the quantum reader corresponds to $k^{\otimes^B}$ regarded as a Frobenius algebra, in fact as a commutative and special Frobenius algebra. In this form the quantum reader monad is prominent in the literature on quantum information theory via dagger-compact categories [Coecke & Pavlović (2008), §1.5.1, Coecke & Paquette (2008), §2.3].

Monoidal monad structure and Decoherence

Proposition

The above quantum reader monad carries the structure of a symmetric monoidal monad with respect to the tensor product of vector spaces (or whatever the tensor product of the given linear types) as follows:

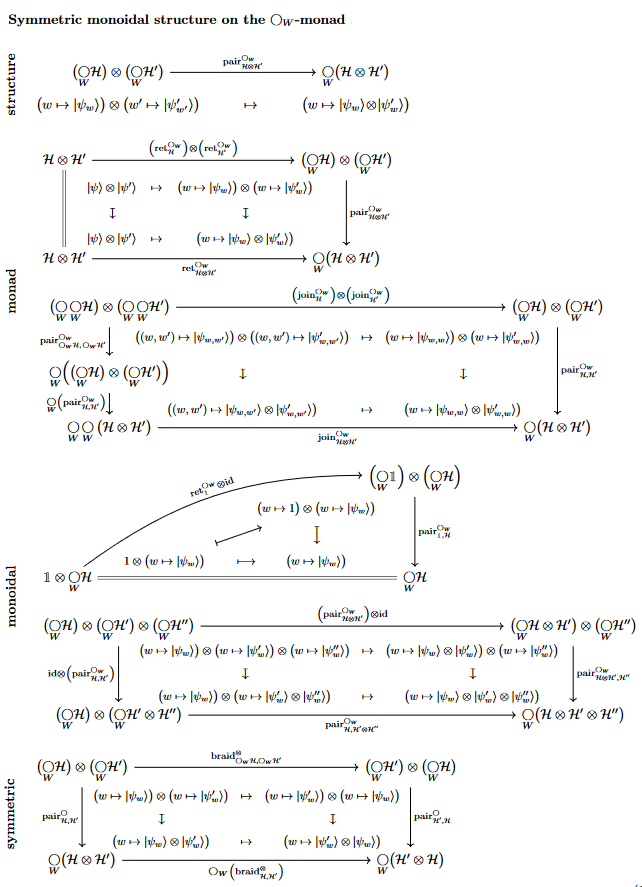
Dually, the quantum coreaders is comonoidal comonadic:

(Here we have assumed strict monoidal structure cf. [Schauenburg 2001], to notationally suppress its associators and unitors.)

Remark

The monoidal monad structure from Prop. extends the above quantum measurement typing from pure states to mixed states, by implementing the decoherence process which eliminates the off-diagonal terms in the density matrix, as indicated in the following:

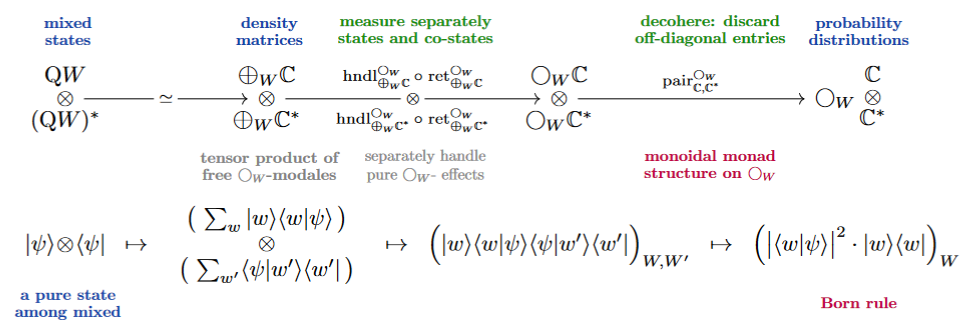
This operation hence sends quantum states (pure or not) to their corresponding probability distributions (under quantum measurement) just as demanded by the Born rule postulate.

Related entries

• quantum costate comonad

• quantum circuits via dependent linear types

• doubly closed monoidal category

References

The quantum reader monad – implicitly, in its incarnation as the $\mathbb{1}^B$-writer Frobenius monad – is highlighted in the literature on quantum information theory via dagger-compact categories as formalizing “classical structures” (namely linear bases for quantum measurement):

• Bob Coecke, Duško Pavlović, §1.5.1 of: Quantum measurements without sums, in: Louis Kauffman, Samuel Lomonaco (eds.), Mathematics of Quantum Computation and Quantum Technology, Taylor & Francis (2008) 559-596 [arXiv:quant-ph/0608035, doi:10.1201/9781584889007]

• Bob Coecke, Eric Oliver Paquette, §2.3 in: POVMs and Naimark’s theorem without sums, Electronic Notes in Theoretical Computer Science 210 (2008) 15-31 [arXiv:quant-ph/0608072, doi:10.1016/j.entcs.2008.04.015]

• Bob Coecke, Eric Paquette, Duško Pavlović, Def. 2.8 in: Classical and quantum structures (2008) [pdf, pdf]

• Bob Coecke, Eric Oliver Paquette, Duško Pavlović, Classical and quantum structuralism [arXiv:0904.1997]

and the evolution of the “classical structures”-monad into the “spider”-ingredient of the ZX-calculus:

• Bob Coecke, Ross Duncan, §3 in: Interacting Quantum Observables, in Automata, Languages and Programming. ICALP 2008, Lecture Notes in Computer Science 5126, Springer (2008) [doi:10.1007/978-3-540-70583-3_25]

• Aleks Kissinger, §§2 in: Graph Rewrite Systems for Classical Structures in $\dagger$-Symmetric Monoidal Categories, MSc thesis, Oxford (2008) [pdf, pdf]

• Aleks Kissinger, §4 in: Exploring a Quantum Theory with Graph Rewriting and Computer Algebra, in: Intelligent Computer Mathematics. CICM 2009, Lecture Notes in Computer Science 5625 (2009) 90-105 [doi:10.1007/978-3-642-02614-0_12]

• Bob Coecke, Ross Duncan, Def. 6.4 in: Interacting Quantum Observables: Categorical Algebra and Diagrammatics, New J. Phys. 13 (2011) 043016 [arXiv:0906.4725, doi:10.1088/1367-2630/13/4/043016]

Also, albeit without explicit mentioning of monadic structures:

• Chris Heunen, Jamie Vicary, around Lem. 5.61 in Categories for Quantum Theory, Oxford University Press 2019 [ISBN:9780198739616]

See also:

• Stefano Gogioso, Finite-dimensional Quantum Observables are the Special Symmetric Dagger-Frobenius Algebras of CP Maps, EPTCS 394 (2023) 432-441 [arXiv:2110.07074]

The above discussion follows:

• Hisham Sati, Urs Schreiber, The Quantum Monadology [arXiv:2310.15735]